Jak to obliczyć?
Czy to jeszcze moduł czy już wartość bezwzględna |z-1| ?
W odpowiedzi z=2
W sumie tak, ale jak robię
pod pierwiastkiem: x2 + y2 + (-1)2
To nie wychodzi.
Co oznacza ta pozioma kreska nad literą Z? Nie kojarzę takiego zapisu.
Tak to robię, zakładając, że -1 też jest w module.
Niestety nie wychodzi i nie mam pomysłu jak inaczej można by to rozwiązać.
Lata temu uzywalem liczb zespolonych, wiec moge pisac glupoty, ale o ile dobrze pamietam to jesli |z| = sqrt(x2+y2) to twoj pierwiastek chyba nie jest dobrze rozpisany, bo masz |z-1|.
I w tym rzecz, jak inaczej to rozpisać skoro w zadaniu mam |z-1|?
Ponownie: pamietaj ze nie wiem praktycznie nic o zespolonych.
Prosta matematyka prowadzi do tego:
|z-1| = |x+yi-1| = |(x-1)+yi| = sqrt[(x-1)2+y2]
Gdybys nie rozumial skad taki zapis:
-1 to liczba zespolona -1+0i, czyli masz (x+yi)+(-1+0i), teraz grupujesz czesci rzeczywiste i urojone i otrzymujesz (x-1)+(yi+0i) = (x-1)+yi. Zgodnie ze wzorem |z| = sqrt(a2+b2), gdzie z=a+bi, wiec twoje a to x-1, a twoje b to y.
[4] Jeśli dobrze pamiętam to ta kreska to 'nie z', coś jak negacja.
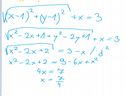
A niech mnie!
O tym nie pomyślałem, dziękuję bardzo nagytow!
Wcześniej próbowałem zrobić coś takiego jeszcze ->
